Extreme weather events cause severe damage. Typical examples are hurricane Sandy and the floods in southern England. Insurance companies need to reserve a sufficient amount of money to cover claims following an extreme weather event. Estimates of expected losses are determined by the tail width of the probability distribution describing the likelihood of extremes. Hence, computing accurate estimates of the tail width is an important challenge for the insurance industry and forecasting agencies.
The so-called Generalized Extreme Value (GEV) distribution describes the distribution of the large values observed in a time series. Using the GEV one can compute the probability of the occurrence of future large values of a quantity, given a sample of past measurements. For that purpose, one must first estimate the parameters of the distribution. Of particular importance is the so-called tail index because it determines the tail width of the distribution and therefore the frequency and intensity of extreme events.
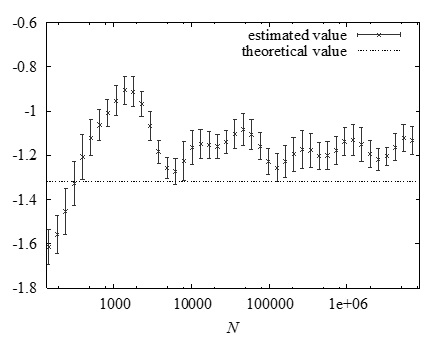
Estimates for the tail index are often obtained by the so-called block maximum method. In this method one divides a time series, either obtained from data or numerical simulations, in sufficiently long blocks. Under the assumption that the block maxima form a random sample drawn from a GEV distribution the parameters can be estimated using standard statistical methods.
For climate models the block maximum method requires very long time series to produce accurate estimates, see Figure 1. Current research aims to develop novel methods to estimate the tail index by means of dynamical indicators such as fractal dimensions. The first results in this direction look promising. The challenge is to extend their applicability to more complicated models eventually also including state of the art climate models.
Contact details
Prof Dr Henk W. Broer
Professor of Dynamical Systems
Johann Bernoulli Institute for Mathematics and Computer Science, University of Groningen
Telephone: +31 50 363 3959
Website: www.math.rug.nl/dsmp/People/HenkBroer
E-mail: h.w.broer@rug.nl
Dr Alef E. Sterk
Assistant Professor
Johann Bernoulli Institute for Mathematics and Computer Science, University of Groningen
Telephone: +31 50 363 3975
Website: www.math.rug.nl/dsmp/People/AlefSterk
E-mail: a.e.sterk@rug.nl








