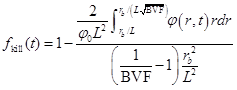Zhihui Wang1,2 and Vittorio Cristini1,2 outline how they have developed a model to help predict cancer treatment outcomes…
The physical properties of a tumour’s microenvironment influence a drug’s ability to penetrate and kill tumour cells. Some of these properties can be potential obstructions to drug diffusion, increasing the tumour’s resistance to chemotherapy. As reported in previous experimental and clinical work, these barriers include overexpression of protein efflux pumps, cell growth cycles, acidosis, hypoxia, tissue density, high interstitial fluid pressure, and electrostatic charge. We argue that diffusion barriers may be another main cause for a tumour’s ability to be drug resistant, and while all of the above factors can contribute to resistance, the drug’s primary challenge is reaching the tumour microenvironment. Whether a drug can be ultimately delivered to the tumour, past the diffusion barriers, depends primarily on the vasculature in the surrounding area and its influence in creating a static environment that prevents perfusion of blood.
Through our integrated mathematical modelling and experimental work (Wang et al., PLoS Computer Biol 2016, PMC4902302), we prove that the key parameters in successfully predicting the amount of cancer cells that will be killed in chemotherapy treatment are the blood volume fraction (BVF) and the radius of the main blood vessels (rb) involved in delivering blood and nutrients to the area. This lays the groundwork for further human clinical studies, specifically in colorectal cancer metastatic to the liver, as well as further research into the contribution of other factors in the microenvironment on drug resistance.
The model is an extension of a previously developed time-dependent drug-cell interaction model (Pascal et al., ACS Nano 2013, PMC3891887) by introducing spatial dependence to describe perfusion and diffusion heterogeneities. The governing equations for drug concentration σ(x, t) and the volume fraction of tumour cells φ(x, t) are
where D is the diffusivity of the drug, λu the per-volume cellular uptake rate of drug, and λk the death rate of tumour cells per unit cumulative drug concentration. This generalised model allows us to examine not only successive (conventional) bolus chemotherapy, characterised by a time-varying intravenous drug concentration according to a specific dosing and timing regimen, but also drug release through loaded nanoparticles where drugs are released at a nearly constant rate over a certain time interval, approximated here by a constant . By integrating the viable tumour volume fraction at each time point over the cylindrical tissue domain surrounding a blood vessel and affected by the drug diffusion, we calculate as the ratio of the killed tumour volume to the total initial tumour volume:
as a function of parameters: rb, blood volume fraction (BVF), and ![]() (the effective diffusion penetration length of the drug).
(the effective diffusion penetration length of the drug).
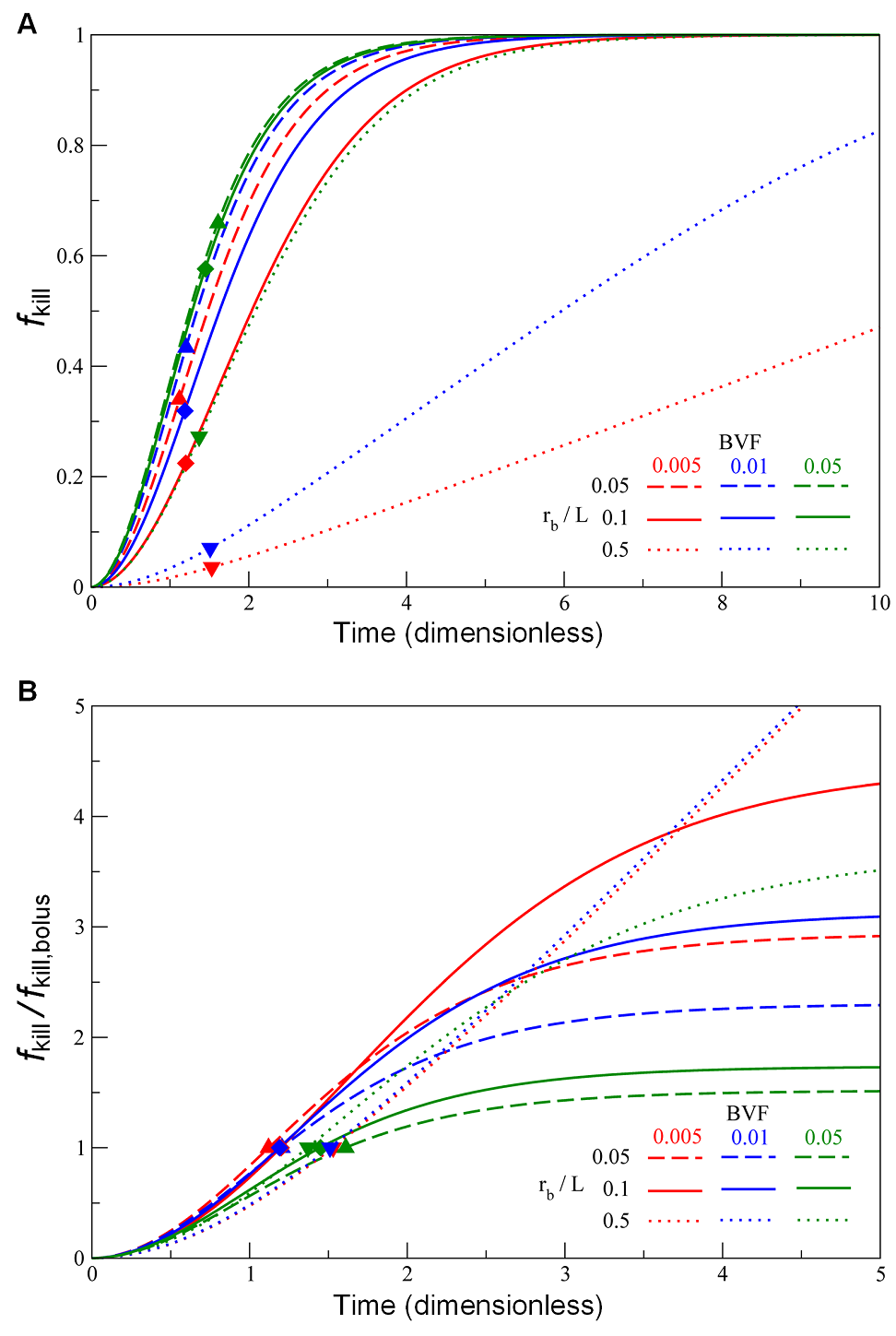
Fig. A shows the temporal evolution curves of ƒkill calculated from Eq. 3 by varying the parameters rb/L and BVF, representing conditions where drug-loaded nanoparticles are employed, as well as the estimates using the previously developed “bolus” model (Pascal et al., Proc Natl Acad Sci U S A 2013, PMC3761643; Frieboes et al., PLoS One 2015, PMC4464754). The results indicate that the “bolus” killing ratios are readily achieved by drug-loaded nanoparticles after 1 or 2 cell cycles. To estimate the benefits of drug release by the nanoparticles over a longer period of time, we normalised the ƒkill curves using their corresponding bolus ƒkill values
Fig. B The results suggest that we may achieve 2- to 4-fold of the bolus killing ratios if the drug release from nanoparticles administration lasts for 3 or 4 apoptotic cycles. However, for large BVF values (representing highly vascularised tumours), cell killing effects from both methods of delivery are roughly equivalent. This suggests an alternative strategy to improve chemotherapeutic efficacy by promoting or normalising angiogenesis at the target site before administrating chemotherapy drugs, or by promoting perfusion by other means such as mild hyperthermia, both of which would lead to an increase in BVF.
1Department of NanoMedicine and Biomedical Engineering, University of Texas Health Science Center at Houston (UTHealth) McGovern Medical School, Houston, TX 77054, USA
2Brown Foundation Institute of Molecular Medicine, University of Texas Health Science Center at Houston (UTHealth) McGovern Medical School, Houston, TX 77030, USA
Additional resources:
http://www.internationalinnovation.com/taking-cancer-out-of-the-equation/
http://www.pnas.org/content/110/35/14266.long
http://www.jci.org/articles/view/73455
Vittorio Cristini, Ph.D.
UTHealth McGovern Medical School Department of Nanomedicine and Biomedical Engineering Center for Advanced Biomedical Imaging (CABI) building
Vittorio.Cristini@uth.tmc.edu
https://med.uth.edu/nbme/faculty/vittorio-cristini/
http://scholar.google.com/citations?user=uwl5tw0AAAAJ&hl=en&oi=ao
Please note: this is a commercial profile