Academic ArticlesThe Standard Model (SM) and the goal of force unification

The Standard Model (SM) and the goal of force unification

The unification of gravitational, Strong and Weak Forces has been a long-sought goal ^[1-3]. In general, force unification refers to the idea that it is possible to view all of the forces of nature as manifestations of one single, all-encompassing force.

Scientists have made great progress toward the goal of understanding how the forces can be combined. Newton realized in the 17th century that the same gravitational force that describes an apple falling from a tree also describes the moon’s orbit around Earth ^[4]. Then, in the 19th century, J. Maxwell demonstrated that electric and magnetic forces are aspects of a single electromagnetic force ^[5]. Finally, in the 20th century, S. Weinberg, A. Salam and S. Glashow showed that, at high energies, the electromagnetic and weak forces merge into a single electroweak force ^[6].

Today, within the context of the Standard Model (SM) of elementary particles, ^[7] scientists seek to unify Gravity with the Strong force under a Grand Unified Theory which binds quarks together and is responsible for the stability of atomic nuclei. These efforts have not been successful yet, most likely because the SM neglects neutrinos ^[8,9], gravity ^[4], special relativity ^[10] and quantum mechanics ^[11].

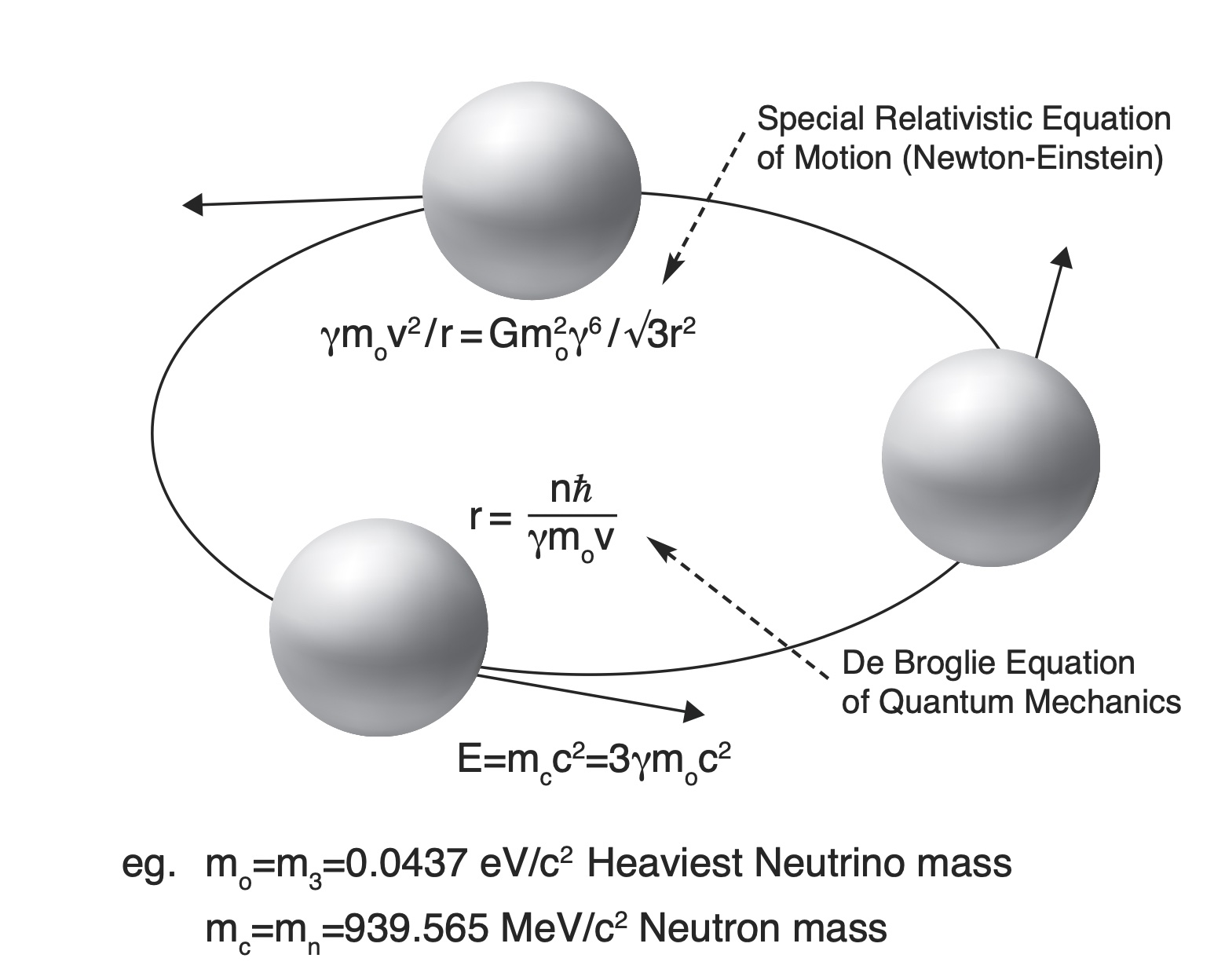
Figure 1. Combining Special Relativity and Quantum Mechanics in the RLM for computing the neutron mass ^[12,13].

Neutrinos and the Rotating Lepton Model (RLM): Mass increases dramatically with speed

The pioneering measurements of Kajita and McDonald ^[8] summarized in ^[9], have shown that neutrinos have mass and exist in three mass eigenstates, namely m₁, m₂ and m₃.

Based on these important measurements a new model, the Rotating Lepton Model (RLM), has been developed. It was first presented in a Springer book in 2012 ^[12], and in numerous other works more recently ^[13-23] and describes the structure of hadrons and bosons ^[13-22] and of the deuteron nucleus ^[23] via gravitating lepton triads rotating in a simple cyclic manner using only Newtonian Mechanics, Special Relativity and the de Broglie equation of quantum mechanics. Figure 1 shows the simplest of these structures, corresponding to the neutron. The structures for other hadrons as well as bosons are shown in Figure 2. For baryons the rotating leptons are m₃ rest mass neutrinos, i.e. the heaviest of the three neutrino types, while for mesons they are m₂ mass neutrinos ^[18]. Finally, bosons contain relativistic electron (or positron)-neutrino pairs ^[14,18]. In this way the RLM computes the speeds, V_i, thus also the Lorentz factors γ_i =(1–V²_I /c² ) ^–1/2 for all the rotating leptons in the composite particle structure under consideration and then it computes its total energy, E_T, and total mass, m_T, via the energy balance equations:

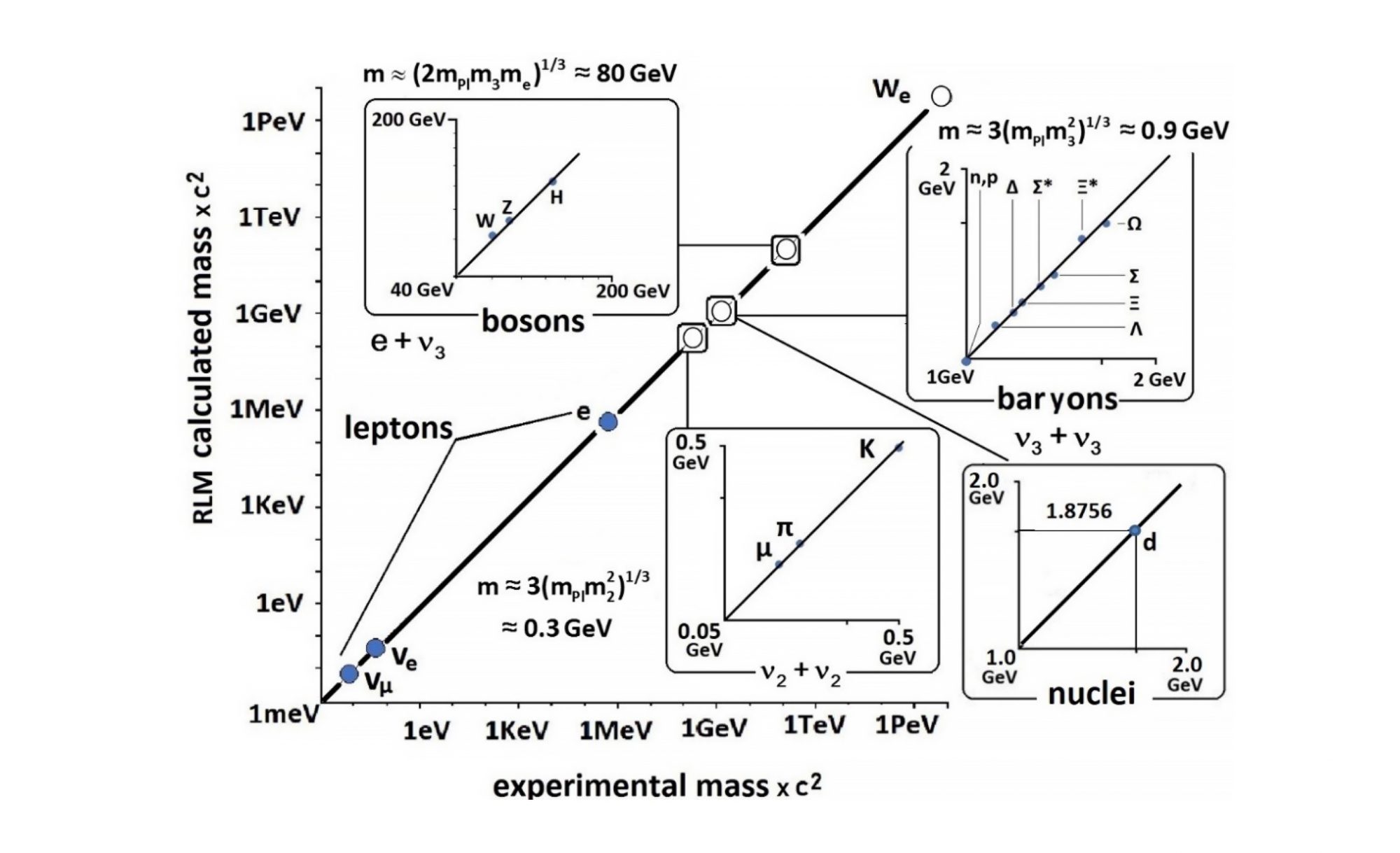
where m_i,o are the rest masses of the rotating leptons. The thus computed composite particle masses m_T differ, amazingly, typically less than 2% from the experimental hadron masses ^[18], as shown in Figure 3.

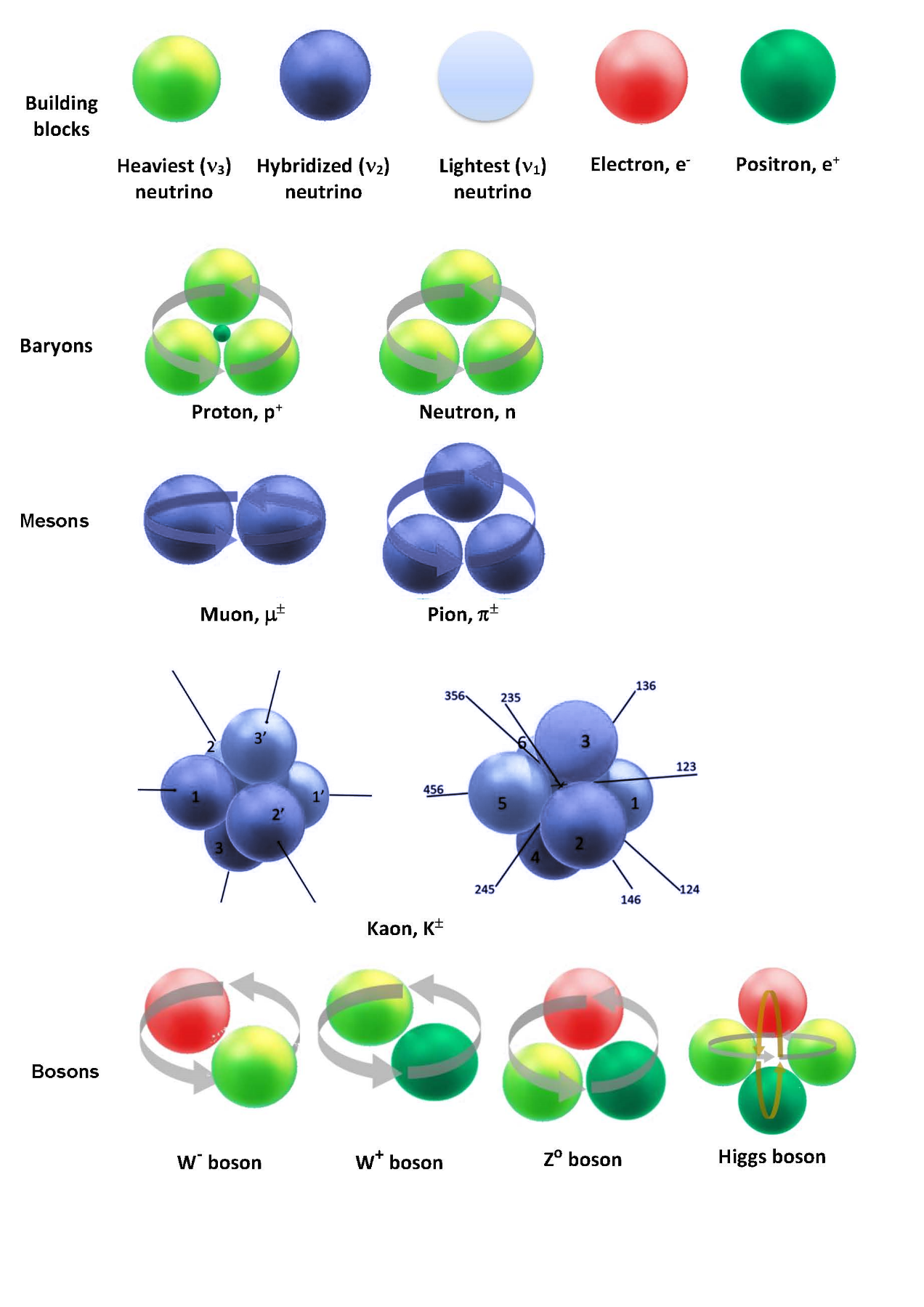
Figure 2. The elementary particles of the Rotating Lepton Model (RLM). (top line) and the RLM structures and composition of baryons, muon, mesons and bosons ^[18].

On the Catalysis of Hadronization

In forming the neutrino or electron/positron-neutrino structures of Figure 2, electrons and positrons, which are quite often good catalysts in Chemistry ^[19] due to their electrostatic interactions, have also played a significant catalytic role, but for a different reason, in hadronization. The reason for their catalytic action in hadronization has been their large, relatively to neutrinos, mass which led and leads to strong gravitational e ± – v interactions during hadronization and to a concomitant pronounced relativistic increase in the neutrino gravitational mass, which equals γ³m_o according to the theory of Special relativity ^[10]. This causes a dramatic 10¹² enhancement in the gravitational attraction between neutrinos and, thus, in the rate of hadronization ^[19].

Quantum mechanics and the de Broglie equation

The computation of the γi values of eq. (1) is achieved by accounting both for special relativity and also for the de Broglie equation

where n is an integer and r is the rotational radius, and by combining then with the equation of motion of each rotating particle. Thus, in the case of a rotating neutrino triad (Figure 1) the equation of motion is

Figure 3. Comparison of the RLM computed masses of composite particles with the experimental values. Agreement is better than 2% without any adjustable parameters. The three approximate mass expressions shown in the Figure provide the order of magnitude of hadron and boson masses ^[18].

Figure 4. Rest masses of the Elementary Particles of the Standard model (SM) ^[7] and of the three neutrino eigenstates ^[8,9]. The arrow shows how the Rotating Lepton Model (RLM) via Special Relativity increases the heaviest neutrino mass from the rest eigenstate mass value m³(~45meV/c²) to the relativistic mass value, γm₃ ≈ 313 MeV/c² of the s quark which corresponds to one third of the neutron formed ^[13].

Upon combining equations (3) and (4) for the ground state (n=1) at the limit v_i ≈ c one obtains

where m_P1=(ħc/G)^1/2=1.221.10²⁸eV/c² is the Planck mass and m_o=m₃ =43.7meV/c2 is the heaviest neutrino eigenmass ^[9]. As depicted in Figure 4 the thus computed very large γ values raise the relativistic neutrino mass (γm_o) values from the range of 10^–1 eV/c²(which is typical for neutrino rest masses) to the range of 1GeV/c²(=10⁹eV/c²) which is typical of protons and neutrons ^[7], thus causing the formation of these hadrons, i.e. thus causing hadronization ^[12]. Consequently, hadronization occurs via the combination of equations (3) and (4), i.e. via the combination of quantum mechanics and special relativity to form stable rotating neutrino triads (Figure 4).

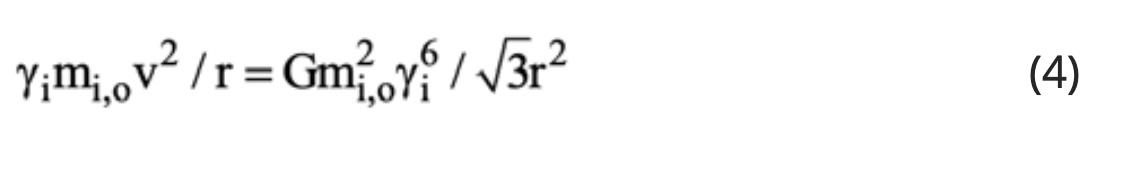
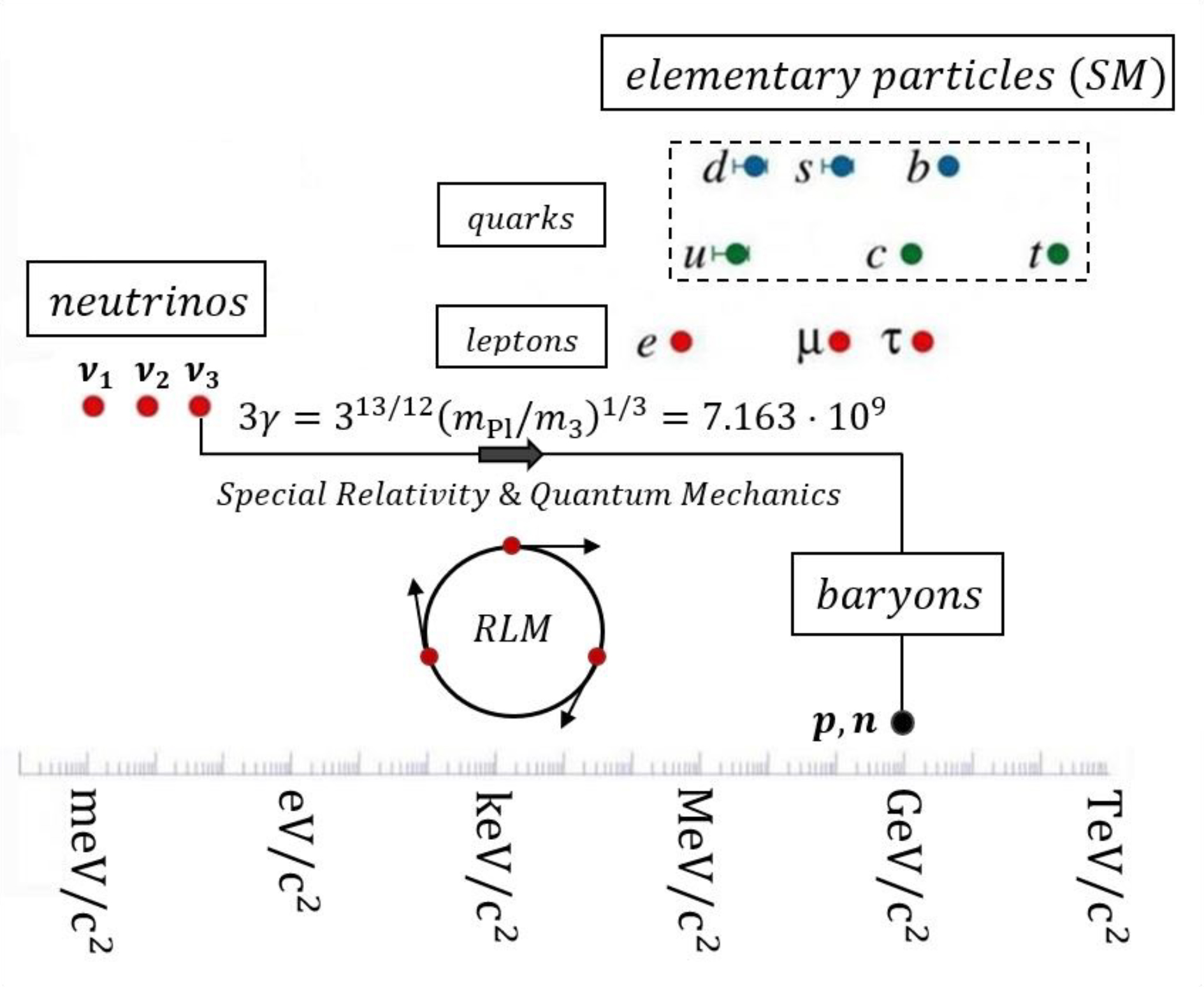
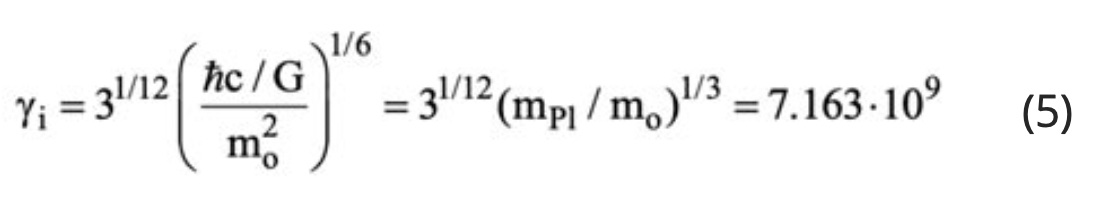
Force Unification

Equation (5) provides the means to unify the Strong and the gravitational forces. Thus, upon substituting equation (5) into the Newtonian gravitational Law using relativistic gravitational masses m_g(=γ³m_o) rather than rest masses, one obtains

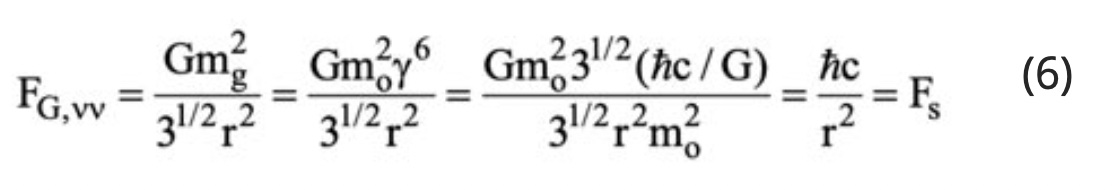
which is the expression for the Strong Force ^[7]. Thus equation (6) unites classical gravity (γ=1) and the Strong Force (γ=3^1/12(m_P1/m_o)^1/3=7.163.10⁹) or equivalently

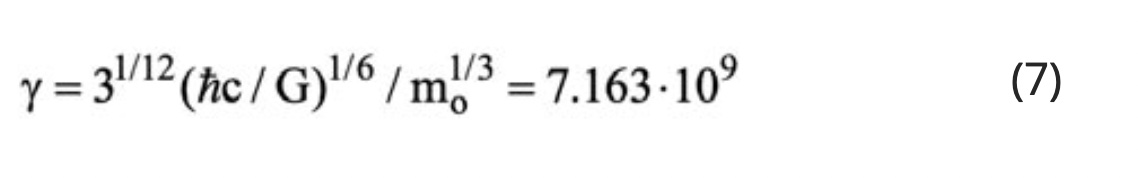
which is equation (5). This unification can also be observed in Figure 5 which examines the dependence of the gravitational force, F_G,νν, between two m₃ type neutrinos on their energy E.

Using (6) and E=γm_oc² to express γ and accounting for

it follows that

which is plotted in Figure 5 vs the particle energy E.

Figure 5. Comparison of the dependence on E at any fixed distance, of the ratios of Coulombic force F_ee of a positron-electron pair and of the gravitational forces between two neutrinos, F_G,νν, and between an electron and a neutrino, F_G,νe, all divided by the strong force F_S=ħc/r² computed from equations (6) and (9); Points n and W± correspond to the energy of formation (baryogenesis) of neutrons (i.e. of quarks with effective mass m_n /3=313 MeV/c² ) and of W± bosons ^[14,18].

One observes that F_G,νν reaches the value ħc/r² at the energy, m_nc² (313 MeV) of a quark in the neutron. The same figure shows the dependence of the gravitational force, F_G,νe, between a relativistic rotating e–ν₃ pair which is known to describe and model the W bosons ^[14,18]. One observes that F_G,νe reaches the value ħc/r² at the energy, m_wc² (=81.74 w GeV) of the W bosons. In summary, as shown in Figure 5, Strong and Weak forces get united with Newtonian (γ=1) gravity at the energies, respectively, of formation of the neutron (0.939 GeV) and of the W boson (81.74 GeV) ^[18]. At higher energies these composite particles decompose.

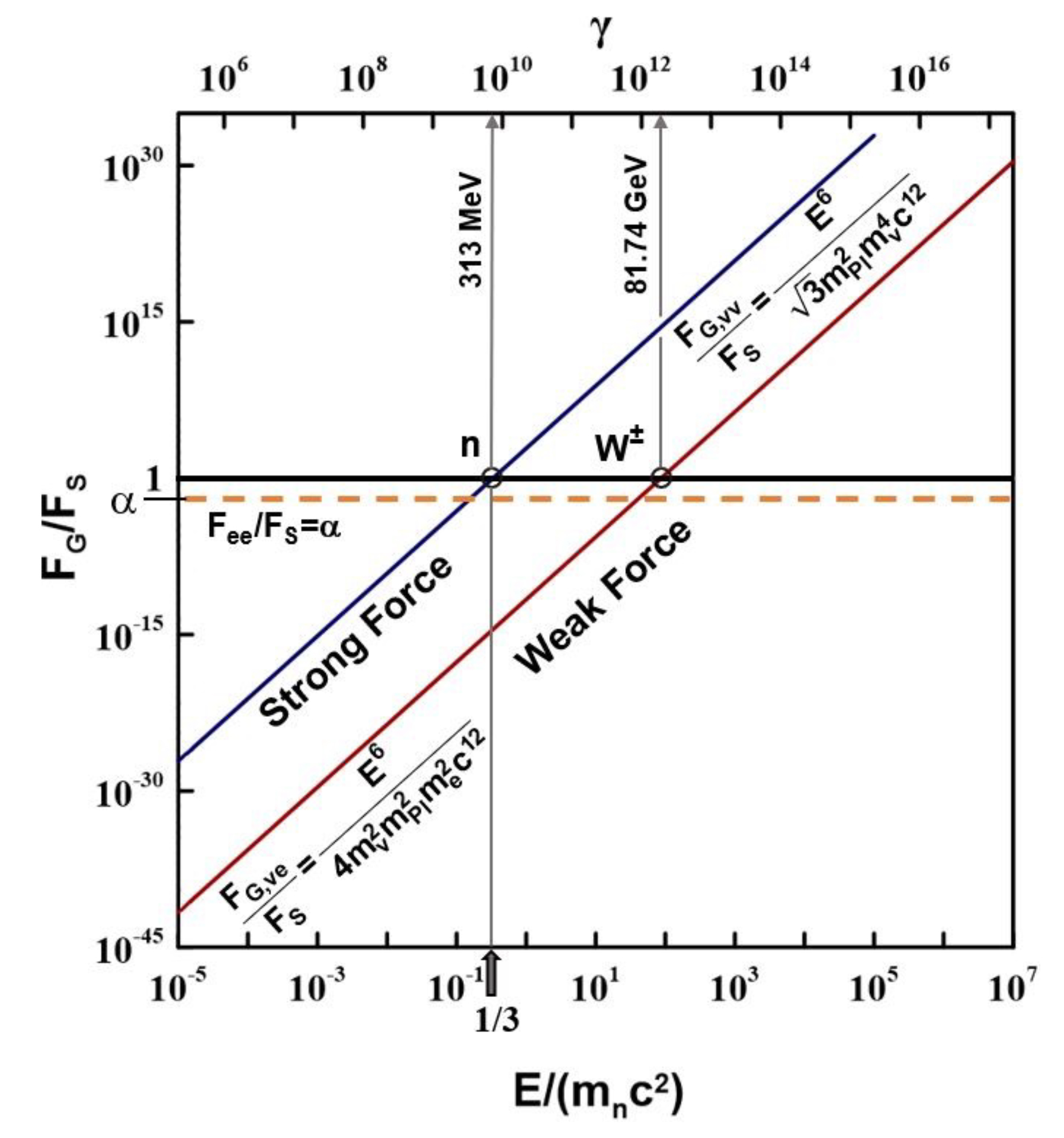
Conclusions on force unification

The Rotating Lepton Model (RLM) explains in a simple and semiquantitative manner the internal structure of hadrons and bosons and allows for the computation of their masses with excellent agreement with experiment. It also allows for the unification of Strong, Weak and Gravitational forces. Its success can be attributed to the fact that it fully utilizes gravity, special relativity and quantum mechanics.

References

S. Weinberg. Dreams of a Final Theory, Pantheon Books (1992).
R. Penrose. The Road to Reality: A Complete Guide to the Laws of the Universe, Vintage, London (2006).
S. Hawking. A Brief History of Time, Transworld Publishers Ltd, London (2011).
I. Newton. Philosophiæ Naturalis Principia Mathematica (1686).
J. C. Maxwell. A dynamical theory of the electromagnetic field. Philosophical Transactions of the Royal Society of London. 155: 459–512 (1865).
S. L. Glashow, Towards a unified theory: Threads in a tapestry, Rev. Mod. Phys., 52:539– 543, 1980
D. Griffiths, Introduction to Elementary Particles. 2nd ed. Wiley-VCH Verlag GmbH & Co. KgaA, Weinheim, 2008.
Kajita, T. Discovery of neutrino oscillations. Rep. Prog. Phys. 2006, 69, 1607–1635.
Mohapatra, R.N.; Antusch, S.; Babu, K.S.; Barenboim, G.; Chen, M.-C.; De Gouvêa, A.; De Holanda, P.; Dutta, B.; Grossman, Y.; Joshipura, A.; et al. Theory of neutrinos: A white paper. Rep. Prog. Phys. 2007, 70, 1757–1867.
French, A.P. Special Relativity; W.W. Norton & Co.: New York, NY, USA,1968.
De Broglie, L.: Waves and Quanta. Nature 112, 540 (1923).
C.G. Vayenas & S. Souentie, Gravity, special relativity and the strong force: A Bohr- Einstein-de-Broglie model for the formation of hadrons. Springer, New York (2012).
Vayenas, C.G.; Souentie, S.; Fokas, A. A Bohr-type model of a composite particle using gravity as the attractive force. Phys. A 2014, 405, 360–379.
Vayenas, C.G.; Fokas, A.S.; Grigoriou, D. On the structure, masses and thermos-dynamics of the W± bosons. Phys. A 2016, 450, 37–48.
Fokas, A.S.; Vayenas, C.G.; Grigoriou, D.P. On the mass and thermodynamics of the Higgs boson. Phys. A 2018, 492, 737–746.
Vayenas, C.G.; Grigoriou, D.P. Hadronization via gravitational confinement. In Proceedings of Particle Physics at the Year of 25th Anniversary of the Lomonosov Conferences, Moscow, Russia, 24–30 August 2017; Studenikin, A., Ed.; World Scientific: Singapore, 2019; pp. 517–524.
Grigoriou, D.P.; Vayenas, C.G. Schwarzschild geodesics and the strong force. In Proceedings of the Particle Physics at the Year of 25th Anniversary of the Lomonosov Conferences, Moscow, Russia, 24–30 August 2017; Studenikin, A., Ed.; World Scientific: Singapore, 2019; pp. 374-377.
Vayenas, C.G.; Tsousis, D.; Grigoriou, D. Computation of the masses, energies and internal pressures of hadrons, mesons and bosons via the Rotating Lepton Model. Phys. A 2020, 545, 123679.
C.G. Vayenas, A.S. Fokas, D. Grigoriou, “Catalysis and autocatalysis of chemical synthesis and of hadronization”. Appl. Catal. B, 203, 582-590 (2017).
Vayenas, C.G.; Tsousis, D.; Grigoriou, D.; Parisis, K.; Aifantis, E.C. Hadronization via gravitational confinement of fast neutrinos: Mechanics at fm distances. Z. Angew. Math. Mech. 2022, 102, e202100158. https://doi.org/10.1002/zamm.202100158.
Vayenas, C.G.; Grigoriou, D.; Tsousis, D. Mass generation via gravitational confinement of fast neutrinos, arXiv:2001.09760v5 (2021).
C.G. Vayenas, D. Tsousis, D. Grigoriou, K. Parisis and E. Aifantis, “Rotating Lepton Model of Pions and Kaons: Mechanics at fm distances”, J.Appl. Math Phys, 10, 2805-2819 (2022).
C.G. Vayenas, D. Grigoriou, D. Tsousis, K. Parisis and E.C. Aifantis, “Computation of the deuteron mass and force unification via the Rotating Lepton Model”, Axioms 11, 657 (2022). https://doi.org/10.3390/axioms11110657.

Please Note: This is a Commercial Profile

This work is licensed under Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International.

Article Categories
Fundamental Research

Publication Tags
OAG 037 - January 2023

Stakeholder Tags
SH Department of Chemical Engineering - University of Patras

The Standard Model (SM) and the goal of force unification

The unification of gravitational, Strong and Weak Forces has been a long-sought goal ^[1-3]. In general, force unification refers to the idea that it is possible to view all of the forces of nature as manifestations of one single, all-encompassing force.