Rotating Lepton Model: Coupling relativity, quantum mechanics and neutrinos for the synthesis of matter

Professor Costas Vayenas and his coworkers Dionysios Tsousis and Dimitrios Grigoriou, discuss how using special relativity to study neutrino motion at fm distances leads to Bohr type models with relativistic gravity as the attractive force

For the last fifty years, the Standard Model (SM) of particle physics has provided the basis for describing the structure and composition of matter. According to the SM, protons and neutrons, which belong to the hadron family of composite particles and are the components of atomic nuclei, consist of elementary particles called quarks which are kept together by a force named Strong Force. ⁽¹⁾ No quarks have ever been isolated and studied independently, and their masses are estimated to be comparable to those of baryons, i.e. of the order of 1 GeV/c². These masses are 100 billion times ^(10,11) larger than the masses of neutrinos (10^-1 to 10^-3 eV/c^{2) (2)} which are the lightest by far, as well as the most numerous, particles in our Universe.

Inertial and gravitational mass increase with speed

Einstein’s theory of Relativity (both special (SR) ^(3,4) and general (GR) ⁽⁵⁾) is one of the most remarkable scientific achievements in the history of humanity. SR has been confirmed experimentally thousands of times and there have been also numerous confirmations of GR. Most confirmations refer to macroscopic systems and only recently ⁽⁶⁾ the amazing strength of SR and GR has been demonstrated inside hadrons, deep in the femtocosmos of the lightest elementary particles, i.e., of neutrinos.

Space contraction, time dilation and mass increase with particle speed are the main features of SR, as the particle speed with respect to an observer, at rest with the centre of rotation, approaches the speed of light c and thus the Lorentz factor γ, defined from γ = (1 – v² / c²) –^1/2, approaches infinity.

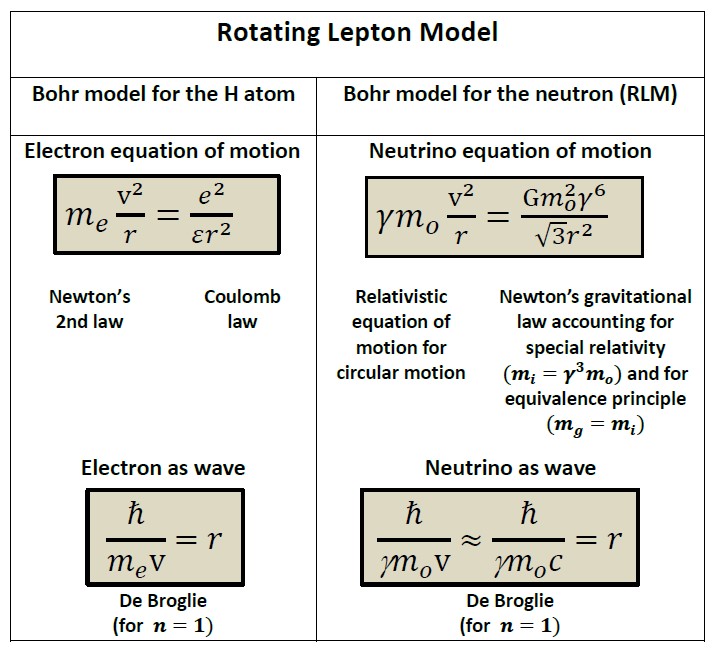
Thus, upon considering three particles rotating symmetrically on a cyclic trajectory using their gravitational attraction, FG, as the centripetal force, then FG can become surprisingly strong. This is because SR dictates that a particle of rest mass mo has a relativistic mass γmo, ^(3,4) and a longitudinal inertial mass γ³mo, equal according to the equivalence principle ^(6,7) with its gravitational mass γ³mo.^(7,8) Therefore, using the definition of the gravitational mass in Newton’s gravitational law it follows:

F_G = Gm²_oγ⁶ / (√3r²)                (1)

where r is the rotational radius. To find r and γ one must also use the de Broglie equation of Quantum Mechanics:

γm_ovr = nћ                               (2)

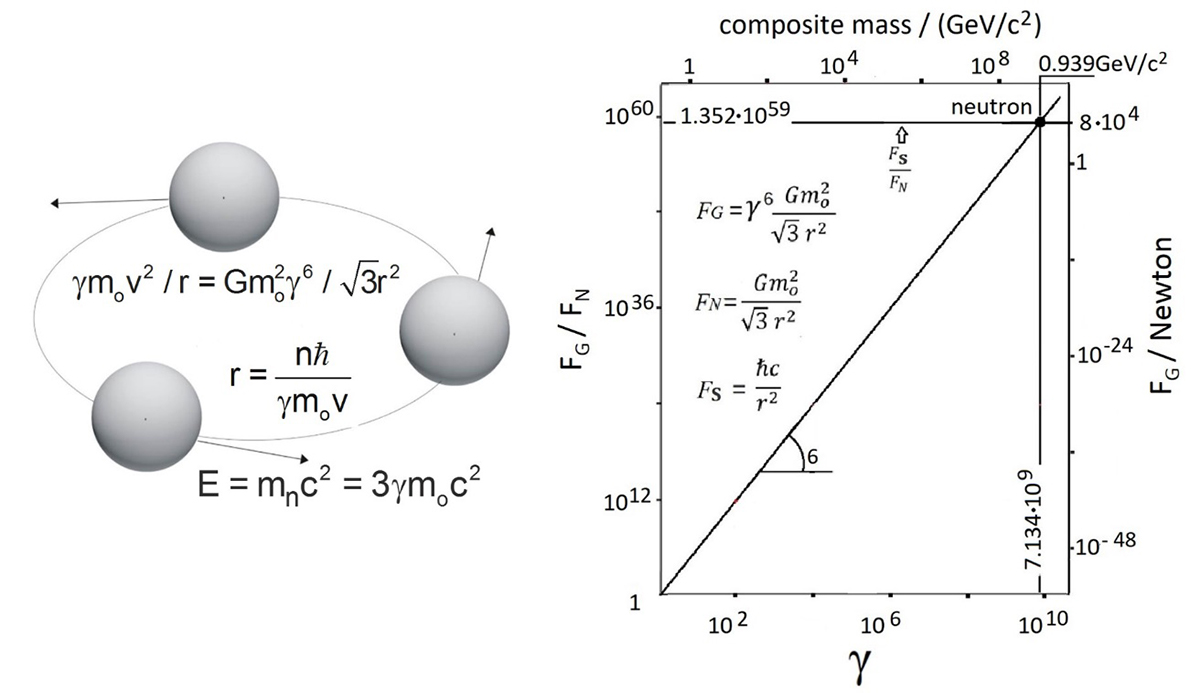
This is used to obtain for n=1 and mo≈43.7 meV/c², estimated ^(6,8) from the Superkamiokande measurements, ⁽²⁾ that r≈0.63 fm and γ≈7.163.10⁹, thus γ6≈1.35.10⁵⁹. Consequently, the rotating speed is very close to c and the gravitational force is, amazingly, according to equation (1), 59 orders of magnitude larger than normal nonrelativistic Newtonian force! (Fig. 1) This force equals 8.10⁴ N, equal to the weight of 100 humans on earth.

Relativistic mass increase: Neutrinos, Quarks and Hadrons

In addition to causing such an astounding γ⁶~10⁵⁹ times increase in gravitational attraction, special elativity also causes an amazing γ ~ 7.168.10⁹ increase in the mass of the three rotating neutrinos so that the composite particle mass increases from 3(43.7 meV/c²) to the neutron mass of 939.565 MeV/c² (Fig. 1). Conversely, if the composite particle mass, 3γmo, is that of a neutron (939.565 MeV/c²) then the rest mass, mo, of each rotating particle is that of the heaviest neutrino eigenmass, ⁽⁹⁾ i.e. 43.7 meV/c², in good agreement with the Superkamiokande measurement of the heaviest neutrino mass. ⁽²⁾ Therefore, special relativity reveals that quarks are relativistic neutrinos and also shows that the neutrino gravitational mass, γ3mo, is enormous, i.e. of the order of the Planck mass (ћc/G)^1/2 = 21.7 mg per neutrino! It thus also implies, in conjunction with equation (2), that the gravitational force of equation (1) equals the strong force, ћc/r², which is a factor of 137 stronger than the electrostatic force of positron -electron pair at the same distance. ⁽¹⁾

Energy minimisation and Hadron mass computation

The RLM shows that maximisation of the Lorentz factor γ leads to enhanced composite particle stability by minimizing –5γm_oc²,  which is the potential energy of the rotating neutrino triad ⁽⁸⁾ and, at the same time by maximising the Lorentz factor γ and thus also the produced hadron mass m = 3γmo = 3^13/12 (mP1mo²)^1/3, where mP1 is the Planck mass (=(ћc/G)^1/2 = 1.22.10²⁸ eV/c²). This simple expression gives, amazingly, a mass value which differs less than 1% from the experimental neutron mass of 939.565 MeV/c².

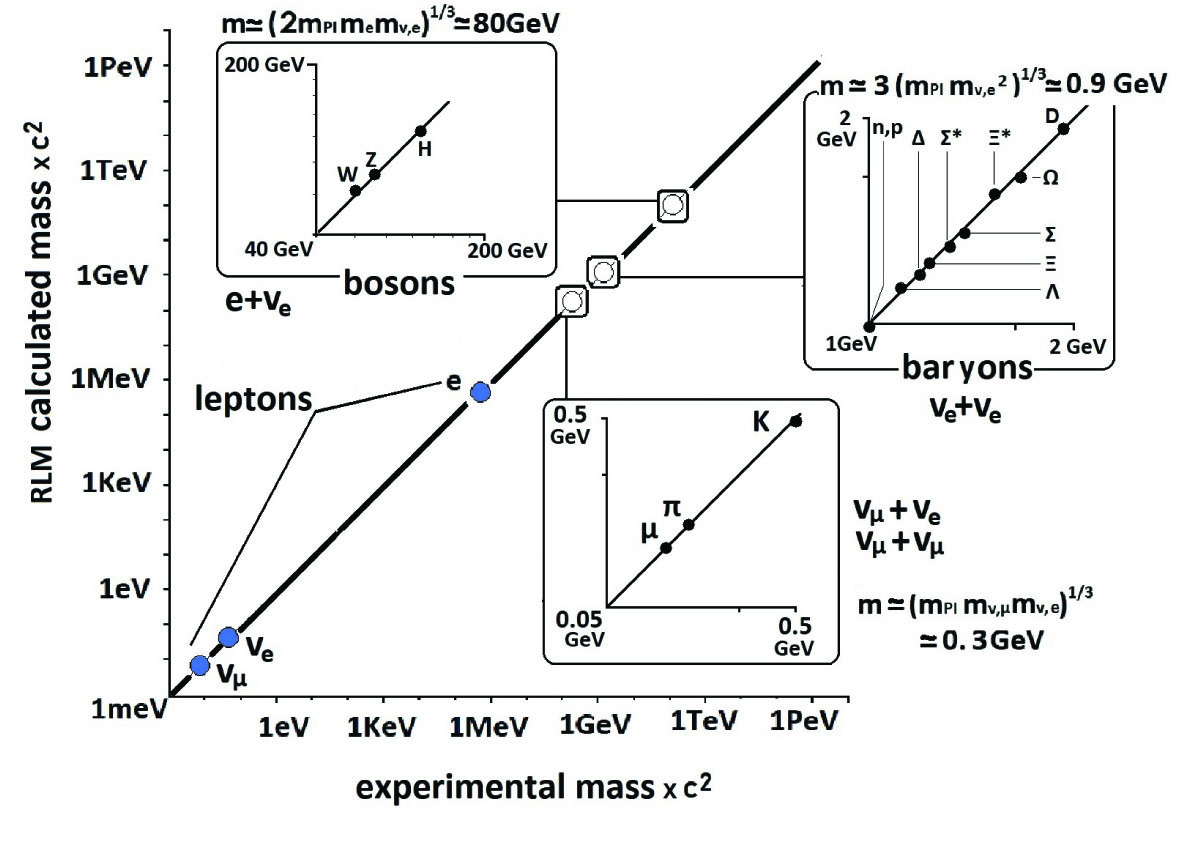
Neutrinos are well known to come in three different “flavours”, i.e. electron neutrinos, muon neutrinos and tau neutrinos. These flavours are obtained by mixing neutrinos from the three mass types (or mass eigenstates), i.e. m₃ mass neutrinos (the heaviest), m₂ mass neutrinos and m1 type neutrinos (the lightest) for the Normal Hierarchy. Using equation (1) and the experimental hadron masses, we have computed the composite particle mass values plotted in Figure 2. Agreement with the experimental composite mass values is better than 2%. Conversely, one may use the experimental hadron or boson mass values to compute the three neutrino masses. Agreement with the experimental values measured at Superkamiokande ⁽²⁾ is within 5%.

Force unification

The fact that the gravitational Newton-Einstein equation (1) provides such a good fit to the experimental mass values of hadrons shows that when accounting for special relativity, gravity suffices to describe the strong force. The equally good fit to the experimental mass values of W±, Z⁰ and H bosons shows that relativistic gravity also suffices to describe the weak force. Indeed, in both cases at the limit of large γ one obtains  F_G = Gm² P1 / r² = G(ћc / G) / r² = ћc/r² whichis the strong force value. ⁽¹⁾ Similarly, for the weak force one also obtains F_G = ћc/r². One may thus conclude that both the strong and the weak forces have been unified with Newtonian gravity (γ=1) in the RLM via equation (1). ^(10,12)

In summary, the RLM reveals that our known Universe is a product of the combination of neutrinos, electrons, positrons, Einstein’s relativity, and the dual wave-particle nature of matter, as described by the de Broglie equation of quantum mechanics. ^(12,13)

References

• Griffiths, Introduction to Elementary Particles. 2nd ed. Wiley-VCH Verlag GmbH & Co. KgaA, Weinheim, 2008.
• Takaaki Kajita, Nobel Lecture: Discovery of Atmospheric Neutrino Oscillations, (2016). Prog. Phys. 69, 1607 – 1635 (2006)
• Einstein (1905) Zür Elektrodynamik bewegter Körper. Ann. der Physik., Bd. XVII, S. 17:891-921; English translation On the Electrodynamics of Moving Bodies (http://fourmilab.ch/etexts/einstein/specrel/www/) by G.B. Jeffery and W. Perrett (1923).
• P. French, Special relativity (W.W. Norton and Co., New York, 1968).
• W. Misner, K.S. Thorne & J.A. Wheeler: Gravitation. W.H. Freeman, San Fransisco, (1973).
• G. Vayenas & S. Souentie, Gravity, special relativity and the strong force: A Bohr-Einstein-de-Broglie model for the formation of hadrons. Springer, New York (2012).
• G. Roll, R. Krotkov, R.G. Dicke (1964) The equivalence of inertial and passive gravitational mass. Annals of Physics 26(3):442-517.
• G. Vayenas, S. Souentie & A. Fokas (2014) A Bohr-type model with gravity as the attractive force. Physica A, 405:360-379.
• G. Vayenas, D. Tsousis and D. Grigoriou, Computation of the masses of neutrinos from the Hadron and Boson masses via the Rotating Lepton model of elementary particles. J. Phys.: Conf. Ser. 1730, 012134 (2021).
• G. Vayenas, D. Tsousis and D. Grigoriou, Computation of the masses, energies and internal pressures of hadrons, mesons and bosons via the Rotating Lepton Model. Physica A, 545, 123679 (2020).
• G. Vayenas, A.S. Fokas, D. Grigoriou, “Catalysis and autocatalysis of chemical synthesis and of hadronization”. Appl. Catal. B, 203, 582-590 (2017).
• G. Vayenas, D. Tsousis, D. Grigoriou, K. Parisis and E. Aifantis “Hadronization via Gravitational confinement of fast neutrinos: Mechanics at fm distances” Zeitschrift für Angewandte Mathematik und Mechanik, https://doi.org/10.1002/zamm.202100158 (2022).
• Halliday, R. Resnick, J. Walker, Fundamentals of Physics, 11th Edition, Wiley (2018).

Please note: This is a commercial profile