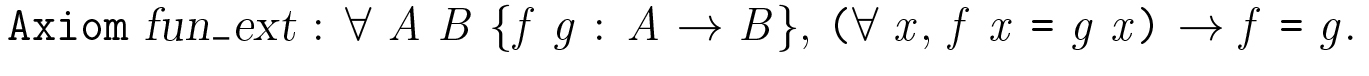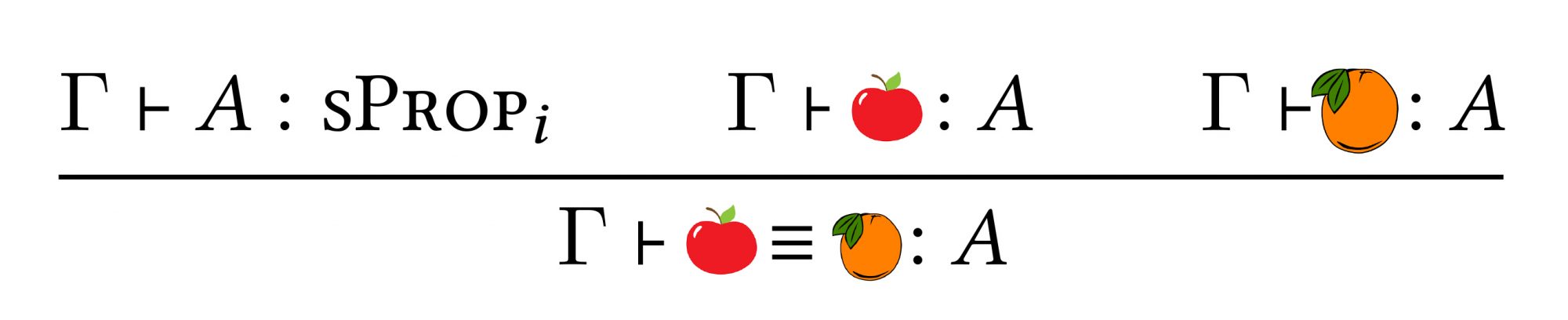Dr Nicolas Tabareau from IMT Atlantique Bretagne-Pays de la Loire, details equality in proof assistants based on type theory, which falls under the umbrella of computer science and mathematics
The Coq proof assistant is a formal proof management system developed by Inria since the early 1990s. It provides a formal language to write mathematical definitions, executable algorithms and theorems together with an environment for semi-interactive development of machine-checked proofs.
Every year, software bugs cost hundreds of millions of euros to companies and administrations, as assessed by Intel Pentium division bug or Ariane 5 first flight failure. Hence, software quality is a notion that becomes more and more prevalent, going beyond the usual scope of embedded systems. In particular, the development of tools to construct software that respect a given specification is a major challenge of current and future researches in computer science. Interactive theorem provers based on type theory, such as Coq, equipped with an extraction mechanism that produces a certified program from a proof, are currently gaining traction towards this direction. Indeed, they have shown their efficiency in proving the correctness of important pieces of software like the C compiler of the CompCert project. One major area of interest when using such theorem provers from a computer science perspective is the ability to extract the code that has been proven directly from the proof – being able to run it as any other pieces of code.
Unfortunately, the democratisation of such interactive theorem provers suffers from a major drawback, that is the mismatch between the conception of equality in mathematics and equality in type theory. Indeed, some basic principles that are used implicitly in mathematics – such as Church principle of proposition extensionality, which says that two formulas are equal when they are logically equivalent – are not derivable in (Martin-Löf) Type Theory. More problematically from a computer science point of view, the basic concept of two functions being equal when they are equal at every “point” of their domain is also not derivable and needs to be set as an axiom (see below).
Of course, those principles are consistent with Type Theory and adding them as axioms is safe. But any development using them in a definition will produce a piece of code that does not compute, being stuck at points where axioms have been used because axioms are computational black boxes. To understand this mismatch, we need to take a deeper look at the notion of equality in type theory. The only way to prove that two terms t and u are equal is by reflexivity, which means that the two terms must be convertible – in the sense that they have the same normal form. To some extent, this notion of equality is eminently syntactic. The reason why this notion of equality is used in type theory is that it comes with a nice elimination principle which allows substituting a term by an equal term anywhere in a type. This is Leibniz’s principle of the indiscernibility of identicals. To the opposite, the notion of equality in mathematics is eminently semantics, with a definition that is relative to the type of terms being considered. This is why the functional extensionality principle is easy to set in this setting because the definition of equality is specialised accordingly when it comes to function types. The problem with that point of view is that it does not come with a generic substitution principle and, thus, is difficult to use it in a programming language. This mismatch prevents proof developments from using more advanced semantical tools in their reasoning because of the explicit manipulation of mathematical equality together with axioms.
The birth of homotopy type theory
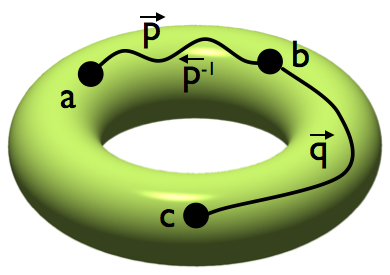
To correct the fundamental mismatch between equality in mathematics and type theory, Martin Hofmann and Thomas Streicher have introduced a new point of view on type theory, where types are not viewed as simple sets but as sets enriched with a homotopical structure. This way, each type comes with a specialised notion of equality and the homotopical structure describes how to substitute a term by another equivalent one in a type. Field medalist Vladimir Voevodsky recognised later that this simplicial interpretation of type theory satisfies a further crucial property, dubbed univalence, which had not previously been considered in type theory. The univalence principle coarsely says that two types (or structures) are equal if and only if they are equivalent (or isomorphic). The univalence principle subsumes the other missing principles of equality and is the key to equip type theory with a notion of equality that is compatible with traditional mathematical reasonings – it is at the heart of Homotopy Type Theory (HoTT).
The first outcomes of HoTT
This new point of view on type theory has now visible consequences in proof assistants such as Coq or Agda. For instance, to give a computational meaning to the univalence axiom, the cubical type theory has been developed by Thierry Coquand and his colleagues and implemented recently in Cubical Agda. In another line of work, a new universe sProp of definitionally proof irrelevant propositions has been implemented both in Coq and in Agda. The development of this notion of proof irrelevance – which guarantees that any two proofs of same proposition A are equal, no matter what they are – would not have been possible without the new insight provided by HoTT. Other outcomes of HoTT will likely be integrated into proof assistants during the coming years.
Please note: This is a commercial profile