Robert Wille, a Professor at the Technical University of Munich and Software Competence Center, discusses the key to data structures when solving quantum computing problems
Quantum computing allows solving certain important problems that were out of reach with classical computers. However, developing applications for this new and upcoming technology has proven to be quite a challenge and requires efficient tools. Data structures are key in this regard: Whenever someone aims to simulate, compile, verify, or debug a quantum algorithm, an efficient representation, e.g., of quantum states or quantum operations is required. Considering that those representations often grow exponentially with respect to the number of qubits, this is not easy. In this article, we provide an overview of data structures for quantum computing available today.
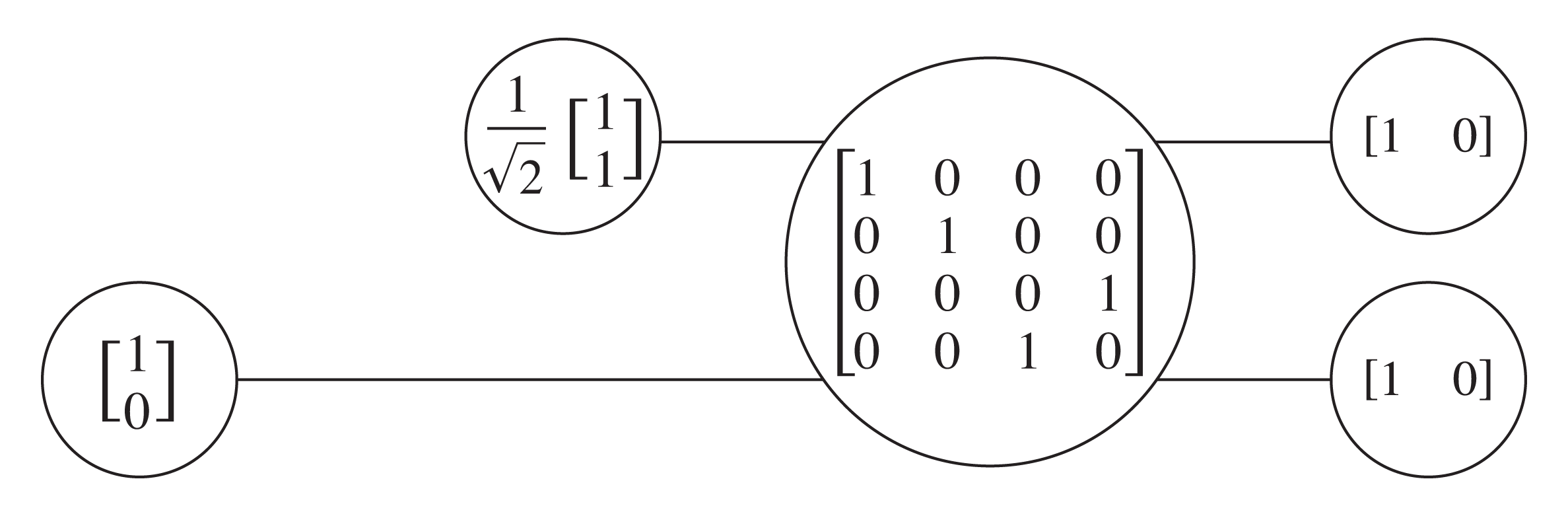
Vectors and Matrices
Vectors and matrices are the most intuitive data structure for quantum computing. They represent quantum states and quantum operations and can be directly realized in the memory of classical computers through 1- or 2-dimensional arrays.
This straightforward realization comes with a prize though: It always leads to an exponential amount of memory. This means that, even with huge supercomputing clusters, the maximum number of qubits that can be represented with them is around 50 – a huge limitation; particularly considering the substantial number of qubits that future quantum computers will work with.
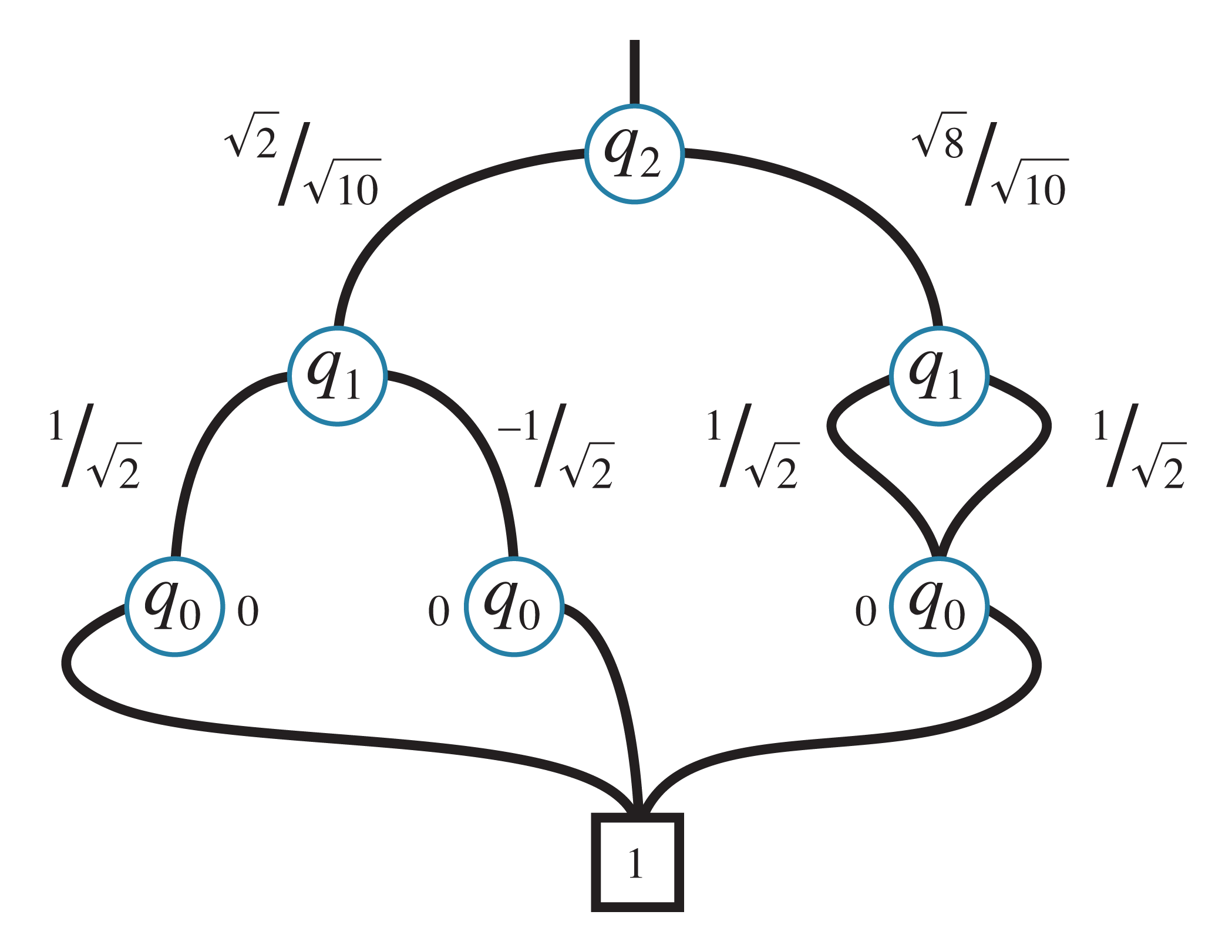
Decision Diagrams
Decision diagrams aim to overcome this exponential complexity by uncovering and exploiting redundancies within the involved quantum states and operations. The underlying vector or matrix is represented as a graph with nodes and edges, where each node corresponds to a part of the vector/matrix.
The compaction comes from sharing: Identical parts of a vector or a matrix (or parts which, e.g., only differ by a common sub-factor) are represented by the same node. The efficacy of the compaction of decision diagrams is highly dependent on the considered quantum state or operation. While there are cases for which decision diagrams hardly provide any reduction, other cases allow to shrink the memory requirements from several terabytes to only a few megabytes.
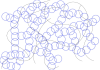
Tensor Networks
Tensor networks can help to alleviate the complexity of representing quantum states and operations by exploiting redundancies in the topological structure of the quantum circuit – instead of the vectors/ matrices. To translate a quantum circuit into a tensor network, each object, be it a state or an operation, is represented by a multi-dimensional array of complex numbers – a tensor. For a circuit, tensors are connected to other tensors according to the underlying quantum circuit. Then, the extraction of useful information from such a tensor network typically requires the pairwise combination of tensors into a single remaining tensor in a process called contraction. Determining an efficient way to contract a given tensor network is one of the main challenges, but eventually can lead to rather compact representations.
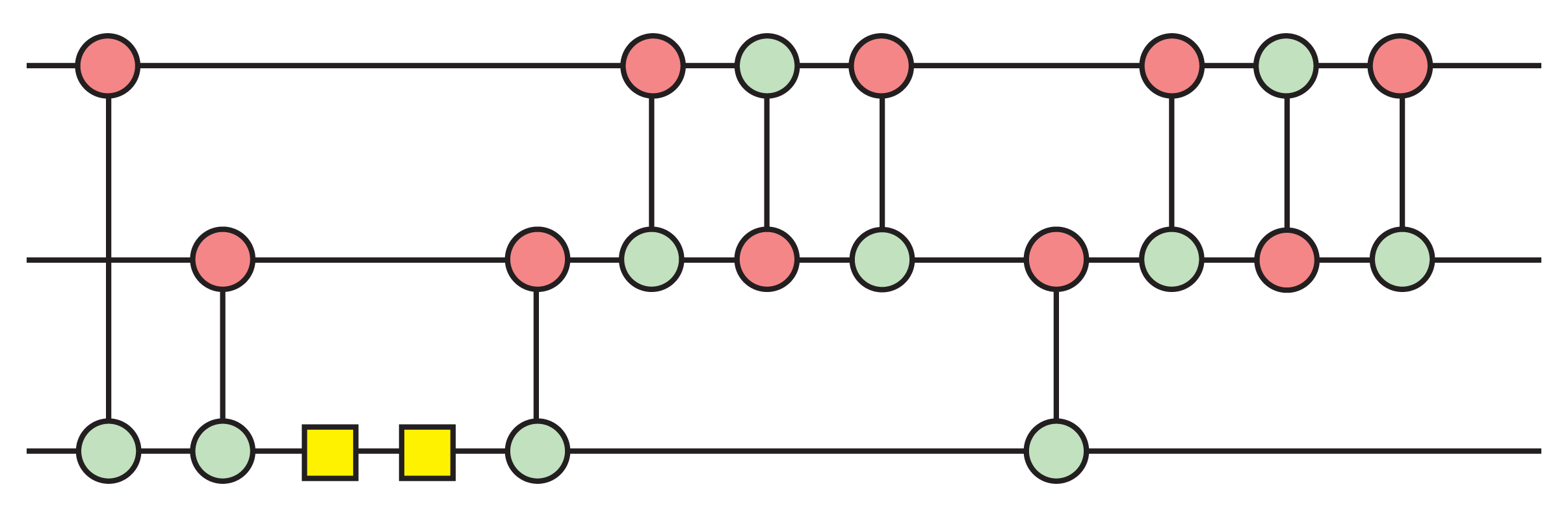
ZX-Calculus
The ZX-calculus is a graphical notation for quantum circuits equipped with a powerful set of rewrite rules that enable diagrammatic reasoning about quantum computing. A ZX-diagram is made up of colored nodes (called spiders) that are connected by wires. An important concept for ZX-diagrams is the only connectivity matters paradigm, which expresses the fact that two ZX-diagrams are considered equal if one can be transformed into the other simply by bending wires.
Any quantum circuit can be interpreted as a ZX-diagram. ZX-diagrams are more general than quantum circuits, however, and allow for representations that do not have meaningful interpretations as quantum circuits. It is this flexibility of being able to leave the quantum circuit formalism that makes the ZX-calculus a good intermediate language when working with quantum circuits.
Interested in More?
The overview above made you hungry for details? Then, check out the following article, which provides more information, explicit examples, and references for further reading: R. Wille, L. Burgholzer, S. Hillmich, T. Grurl, A. Ploier, and T. Peham. The Basis of Design Tools for Quantum Computing: Arrays, Decision Diagrams, Tensor Networks, and ZX-Calculus. In Design Automation Conference (DAC) 2022
The data structures summarized above are heavily used in the Munich Quantum Toolkit (MQT) – an open source software toolkit for quantum computing developed at the Technical University of Munich. Those tools are available at https://github.com/ cda-tum/.
Furthermore, a web-based graphical interface showcasing a lightweight visualization of decision diagrams for quantum circuit simulation and quan- tum circuit verification is available at https://www.cda.cit.tum.de/app/ddvis/.
Try it out today!
Contributor Profile
Editor's Recommended Articles
-
Must Read >> Design tools for quantum computing -
Must Read >> Einstein Telescope: A unique chance for Europe -
Must Read >> Classical simulation of quantum circuits
