Chemistry and biochemistry: Sugar conformational equilibria and dynamics

August 25, 2019

Ian Carmichael^a, Robert J. Woods^b and Anthony S. Serianni^c share their expertise on an aspect of chemistry and biochemistry that concerns circular statistics and NMR which reveal sugar conformational equilibria and dynamics

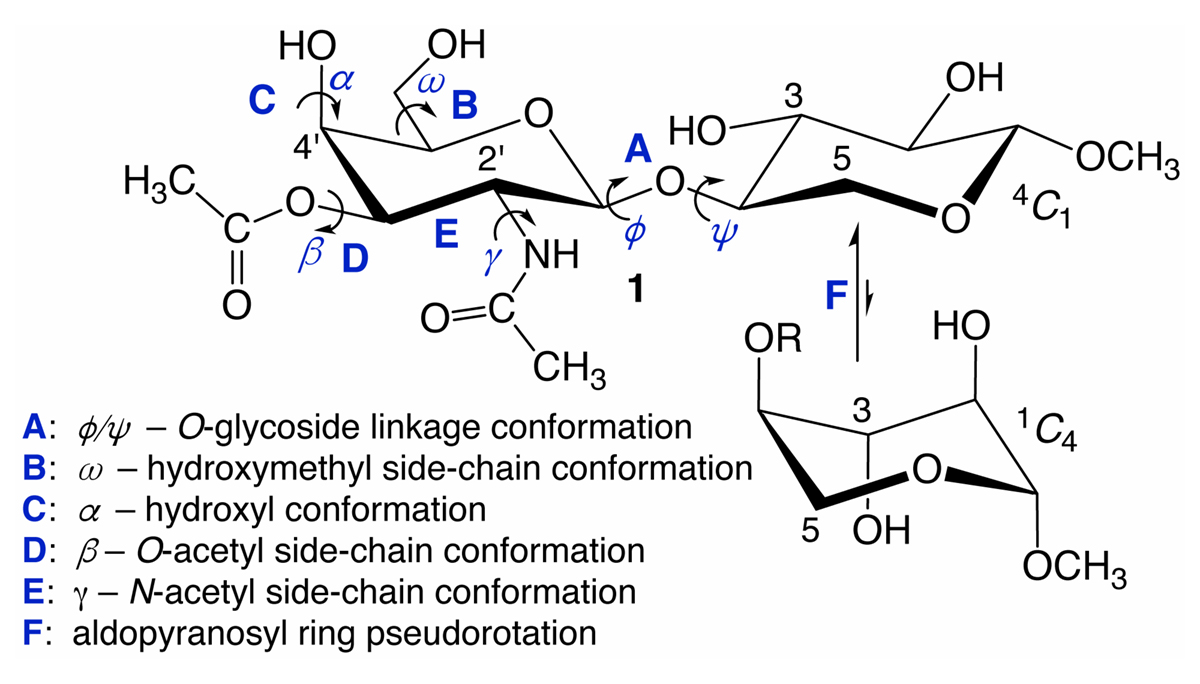
Carbohydrates are talented actors on the biological stage. In addition to their roles in metabolic energy production, they are found on cell surfaces, conjugated to membrane-associated proteins and lipids and as such serve as ligands of extracellular receptors that mediate cellular processes such as cell-cell recognition, bacterial and viral infection, immunity and intracellular trafficking.¹ Sugar conformational equilibria and dynamics can be complex in that saccharides contain multiple, flexible elements that collectively determine their overall shapes in solution. The properties of these flexible elements are often correlated and include pyranosyl ring pseudorotation, exocyclic hydroxyl and hydroxymethyl side-chain rotation, N- and O-acetyl side-chain motions and motions about O-glycosidic linkages in oligosaccharides (Figure 1).

Figure 1. Some common conformational elements in saccharides, illustrated in the disaccharide, methyl 2-acetamido-2-deoxy-3-O-acetyl-β-D-galactopyranosyl-(1→4)-β-D-xylopyranoside (1).

For decades, NMR spectroscopy has been used to characterise these solution behaviours by measuring, for example, nuclear Overhauser effects (NOEs), scalar couplings, residual dipolar couplings and nuclear spin relaxation.² These parameters yield valuable insights into saccharide behaviours but cannot provide, independently, continuous conformational models; their interpretations rely on input from computed energies and/or molecular dynamics (MD) simulations. This dependence is troublesome because (a) saccharide computed energies are error-prone due to the influences of hydroxyl group conformation and/or solvation and (b) saccharide MD simulation models are very difficult to validate experimentally. Current research relies on MD to provide information on saccharide conformation and dynamics in the absence of definitive experimental evidence that MD models provide accurate pictures of solution behaviour.

A new development in the analysis of NMR scalar couplings promises to break the circular arguments and provide independent experiment-based models of saccharide solution behaviour. The technique, known as MA’AT analysis,^3-6 yields outputs very similar to those provided by MD, allowing direct superimposition of MA’AT-derived models on those obtained by MD simulations.

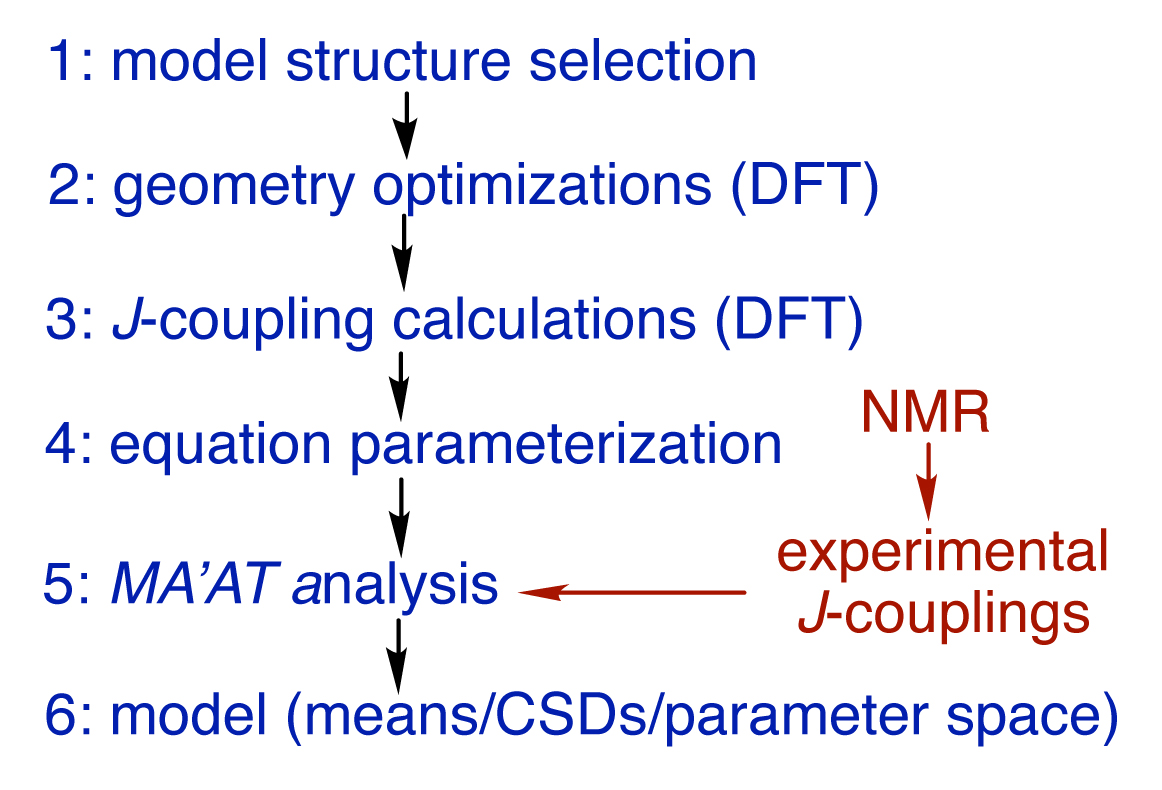
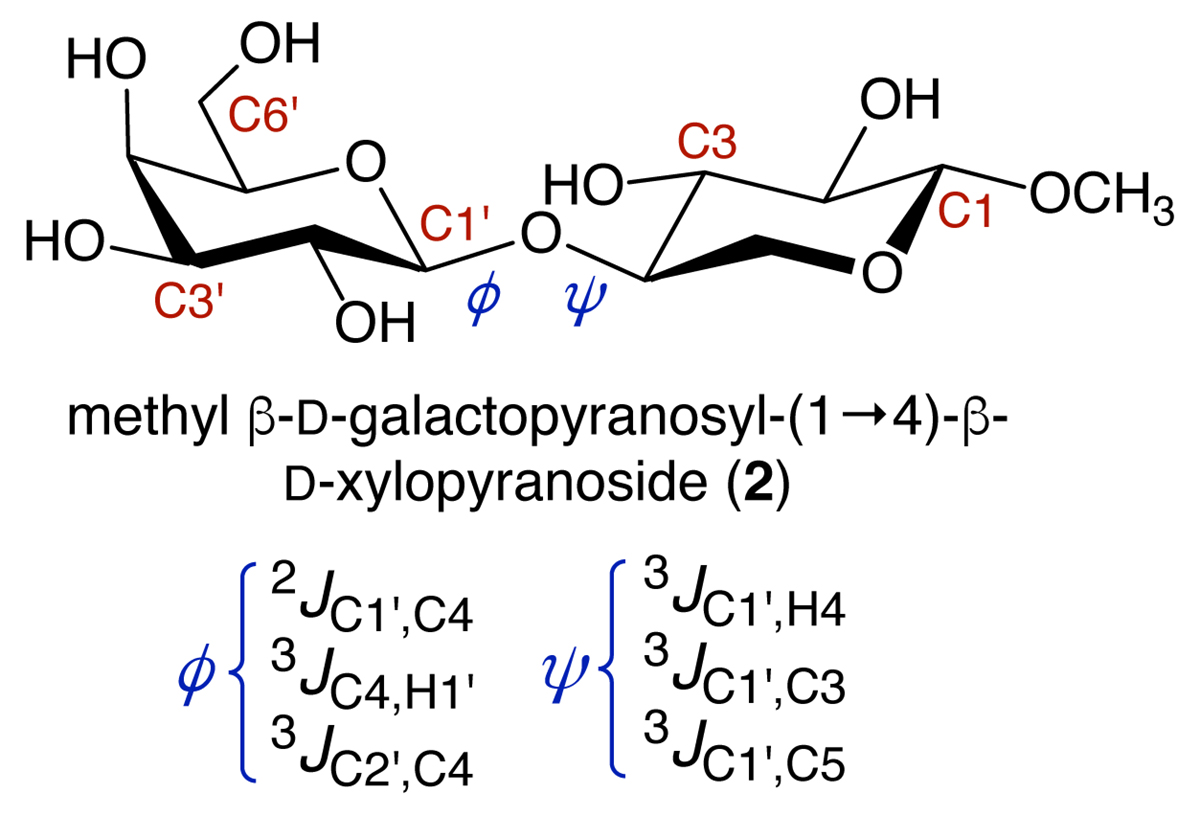
Figure 2. Flow chart for MA’AT analysis. After model selection (1), DFT is used to conduct geometry optimizations (2) and to calculate J-couplings (3). Parameterized J-coupling equations (4) are used along with experimental J-couplings as input to the MA’AT program (5). Conformational models are obtained as output (6).

MA’AT analysis involves six steps (Figure 2), illustrated in the modelling of the phi (ф) and psi (ψ) O-glycosidic torsion angles of disaccharide 2 (Figure 3). The structure of 2 is encoded in the z-matrix input to Gaussian.⁷ Ensembles of redundant J-couplings sensitive to ф and ψ are required and in this case, three J-values are sensitive to each angle (Figure 3). Rotating ф and ψ in the in silico model of 2 through 360° in 15° increments produces 576 conformers and each is geometry optimised using density functional theory (DFT) (Step 2). The six J-couplings are calculated in the 576 conformers (Step 3) and the dependencies are encoded into parameterised equations that generally take the form, J_exp = A + B cos θ + C cos 2θ + D sin θ + E sin 2θ (Step 4). The experimental J-couplings are measured in 2 and the experimental values and parameterised equations are used by the MA’AT program (Step 5), which applies a Monte Carlo search and circular statistics to fit the experimental J-values to conformational models of ф and ψ (Step 6). In this case, only single-state models of ф and ψ pertain due to the small number of observables, but multi-state models can be tested if the number of experimental J-couplings is sufficient (see below). MA’AT outputs include the mean values of ф and ψ and circular standard deviations (CSDs) of these mean values, the latter providing information on the librational character of each torsion angle.

Figure 3. Definitions of ф and ψ in disaccharide 2 and redundant NMR spin-couplings sensitive to these torsion angles.

The application of MA’AT to ф and ψ in 2 gives the single-state models shown in Figure 4(C), superimposed on those determined by aqueous MD simulation. The models are in good agreement for ψ, but differ for ф. The sensitivity of the method can be demonstrated by examining βGal-(14)-βGlcOCH₃ (3) and βGal-(14)-βAllOCH₃ (4) in a similar manner (Figure 4A and B). MA’AT models of ψ in 3 and 4 recapitulate the MD models well, but discrepancies in ф are observed similar to that found for 2.⁴

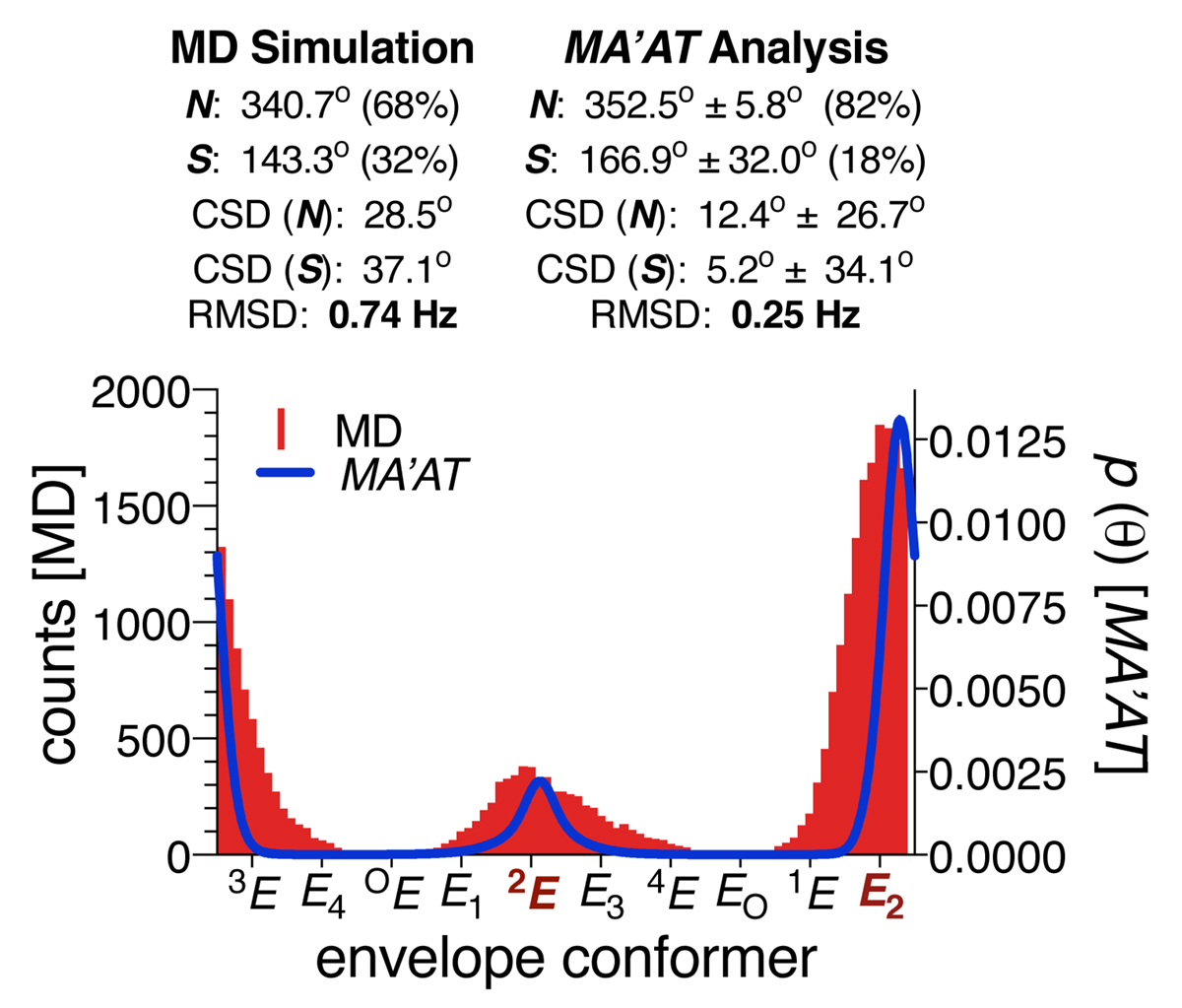
Figure 4. MA’AT and MD analysis of ф and ψ in (A) βGal-(1→4)-βGlcOCH3 (3), (B) βGal-(1→4)-βAllOCH3 (4) and (C) βGal-(1→4)-βXylOCH3 (2), shown as Newman projections down each C–O bond. Histograms (red) were obtained from 1-μs aqueous MD simulations on which are superimposed distributions (blue) determined from MA’AT analysis. Data were taken from ref. 4.

MA’AT analysis can be applied, in principle, to any conformational element in any molecule if multiple, redundant J-values exist, can be measured reliably and can be parameterised. For example, the conformational behaviour of the furanose ring in methyl β-D-ribofuranoside (5) was investigated using nine intra-ring J_HH, J_CH and J_CC values to give a two-state E₂/²E pseudorotational model that recapitulates, although not exactly, that obtained by MD simulation (Figure 5).

Figure 5. MA’AT analysis of methyl β-D-ribofuranoside (5), yielding a two-state E2 / 2E model (blue curve) superimposed on the model predicted by a 1-μs aqueous MD simulation (red histogram). Fitting statistics for both models are shown above the plot. [unpublished]

MA’AT analysis was first described in 2017,^3-4 and its power and applicability have yet to be fully illuminated. It is expected that the method will lead to improved MD force-fields, especially in cases where solvent effects play key roles in determining conformational preference in solution. In addition, while current applications have been limited to saccharides, studies of oligopeptides and oligonucleotides and perhaps larger molecules, are anticipated.

References

1 Varki, A. Glycobiology 2017, 27, 3–49.

2 Blundell, C. D., Reed, M. A. C., Overduin, M., and Almond, A. Carbohydr. Res. 2006, 341, 1985–1991.

3 Turney, T., Pan, Q., Sernau, L., Carmichael, I., Zhang, W., Wang, X., Woods, R. J., and Serianni, A. S. J. Phys. Chem. 2017, B121, 66–77.

4 Zhang, W., Turney, T., Meredith, R., Pan, Q., Sernau, L., Wang, X., Hu, X., Woods, R. J., Carmichael, I., and Serianni, A. S. J. Phys. Chem. 2017, B121, 3042–3058.

5 Zhang, W., Meredith, R., Pan, Q., Wang, X., Woods, R. J., Carmichael, I., and Serianni, A. S. Biochemistry 2019, 58, 546–560.

6 Zhang, W., Meredith, R., Yoon, M.-K., Wang, X., Woods, R. J., Carmichael, I., and Serianni, A. S. J. Org. Chem. 2019, 84, 1706–1724.

7 Frisch, M. J., Trucks, G. W., Schlegel, et al. Gaussian09, Revision E.01, Gaussian, Inc., Wallingford CT, 2009.

[^aRadiation Laboratory and cDepartment of Chemistry and Biochemistry, University of Notre Dame, Notre Dame, IN 46556-5670 USA; ^bComplex Carbohydrate Research Center, University of Georgia, Athens, GA 30602 USA].

This work was supported by the U.S. National Science Foundation (CHE 1402744 and CHE 1707660).

Please note: This is a commercial profile