Evaluating multiple treatments within one study: Some practical considerations

Prof Thomas Jaki, Professor of Statistics at Lancaster University’s Medical and Pharmaceutical Statistics Research Unit tells us about some practical considerations around evaluating multiple treatments for patients

In a multi-arm study, several experimental arms are evaluated within a single trial. The different arms can be different experimental treatments, different doses of the same agent or different combinations of treatments. Most commonly, such designs include a common control group against which each of the experimental arms is compared to. This set-up has the advantage that only a single control group is required so that fewer patients need to be allocated to the control treatment, compared to separate two-arm evaluations. The resulting reduction in sample size for a trial with three experimental arms – versus conducting three separate two-arm trials – is about 15%.

At the same time, a patient’s chance to receive an experimental treatment is increased, which can help with recruiting patients [1]. These studies undertake a contemporary comparison of different experimental treatments using a single protocol – meaning that important features, such as the population studies, are the same.

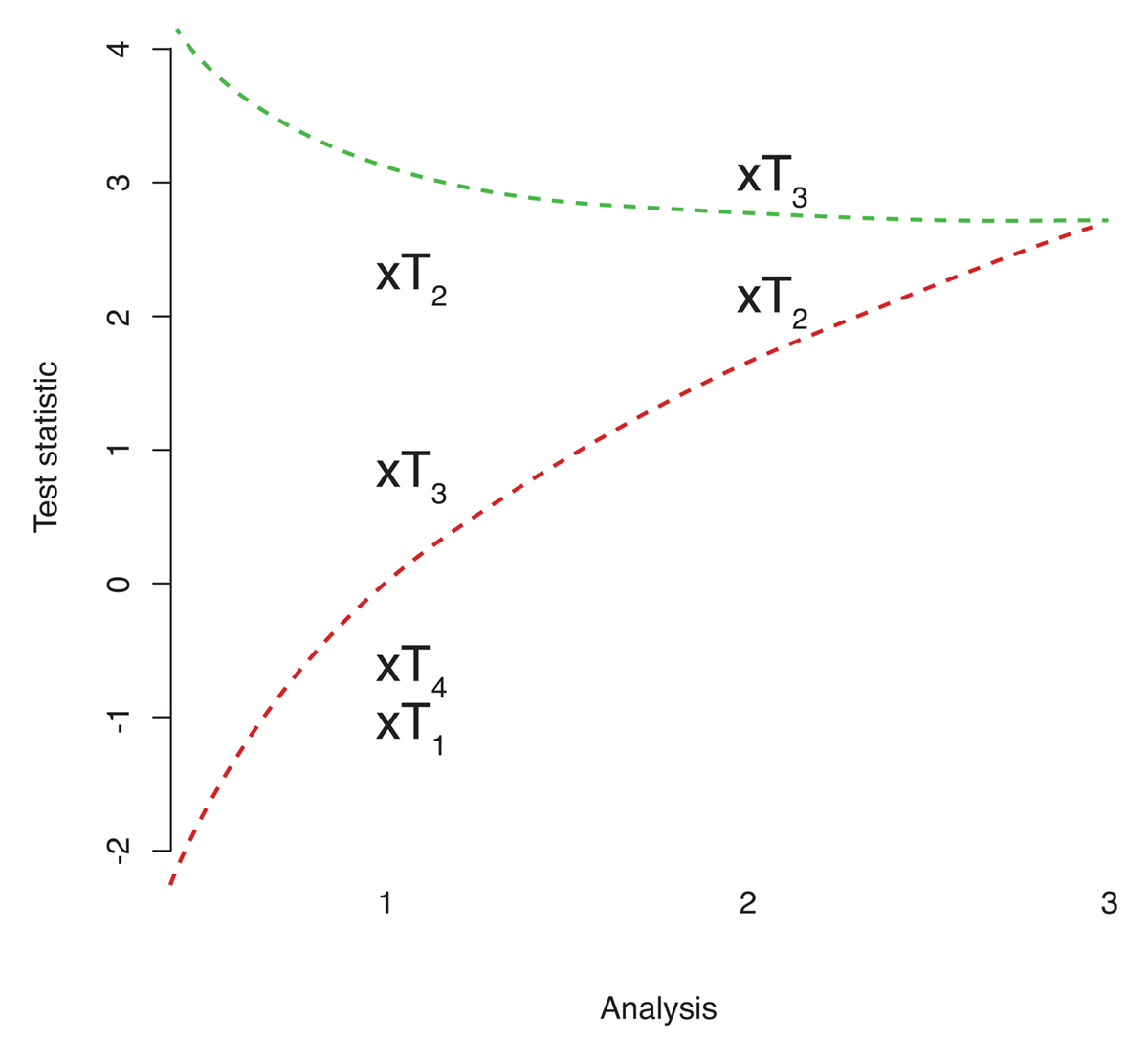
Interim analyses that allow early termination of the study, either because of the proven effect of one treatment or due to a lack of benefit, increase the efficiency of these designs further. In addition, the interim analyses can be used to select which treatment(s) warrant further study. Figure 1 illustrates such a design where treatments are eliminated from the study – should the corresponding test statistic be too small (or equivalently the p-value to large) – that is fall below the lower bound. If the test statistic of one treatment is high – in that it exceeds the upper bound – the trial can be stopped, and the superiority of that treatment is claimed.

In the case where no test statistic is above the upper bound and at least one test statistic falls between the upper and the lower bound, the trial continues with all remaining experimental arms in addition to the control arm. In the schematic of Figure 1, four treatments are compared against a common control and up to three analyses undertaken. At the first analysis, the test statistics comparing treatment 1 vs control and treatment 4, against control fall below the lower bound and hence they are removed from the study. Since none of the test statistics exceeds the upper bound, the study continues with treatments 2, 3 as well as the control group. At the second interim, the test statistic corresponding to treatment 3 exceeds the upper bound and hence superiority of treatment 3 over control can be claimed and the study can be stopped.

Multi-arm trials in practice

We illustrate above that multi-arm studies are efficient. They do, however, also require additional considerations. When comparing multiple arms, all treatments in the study need to be available at the same time to ensure a contemporary evaluation. Additionally, a multi-arm study implicitly assumes that all experimental treatments start on an equal footing – i.e. no treatment is believed to be better than any other before the study starts.

The analysis of a multi-arm study also requires special attention. Using standard analysis methods will result in an overenthusiastic (upward biased) estimate of the effect. Specialised methods for estimation and constructing confidence intervals [e.g. 3] are therefore necessary for analysing such studies.

For multi-arm studies with several analyses, one must note that the maximum sample size required will be larger than for a multi-arm study with a single analysis as the designs need to protect against an increased chance of claiming that a treatment is better than control when it is not. Note, however, that the expected number of patients is typically notably smaller. Even though the increase in the maximum sample size is typically small (<10%), recruiting the maximum number of patients still needs to be possible. For (notable) reductions in the expected sample size, it is crucial that the endpoint used for treatment selection (primary endpoint or some short-term surrogate) is observed quickly since patients will continue to be randomised to each arm while the data to make the interim treatment selection are being collected.

Generally, the conduct of interim analyses must be efficient and to relatively tight deadlines as delays in the selection decision reduces the benefit of such a design. Consequently, the additional resource is often required to facilitate quick decisions and to ensure blinding and trial integrity. Efficient communication between investigators, data management and statisticians are essential.

Communicating the more complex design of multi-arm studies to both patients and investigators also requires some thought. The informed consent procedure requires careful consideration as patients need to be fully aware of all possibilities.

Finally, planning and ensuring treatment supply needs careful thought before embarking on a multi-arm study that allows selection. The maximum amount of a drug required is uncertain as arms can be stopped prior to the end of the study. While the same issue exists for group-sequential designs, the additional arms make this challenge more pronounced. Accurate planning and precise estimation of recruitment rates are paramount.

References

[1] Parmar MKB, Carpenter J, Sydes MR (2014). More multiarm randomised trials of superiority are needed. Lancet. 384(9940), 283-284.

[2] Magirr D, Jaki T, Whitehead J (2012). A generalised Dunnett test for multi-arm, multi-stage clinical studies with treatment

selection. Biometrika. 99(2), 494-501.

[3] Brueckner M, Titman A, Jaki T. (2017) Estimation in multi-arm two-stage trials with treatment selection and time-to-event

endpoint. Statistics in Medicine. 36(20):3137-3153.

CAPTION: Figure 1 Illustration of a multi-arm multi-stage study following [2].

Please note: this is a commercial profile

Prof Thomas Jaki

Professor of Statistics

Medical and Pharmaceutical Statistics

Research Unit

Lancaster University

Tel: +44 (0)1524 59 23 18

mps@lancaster.ac.uk

www.mps-research.com